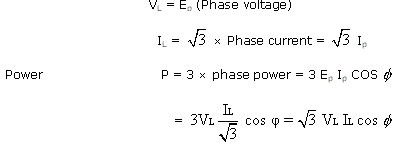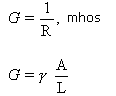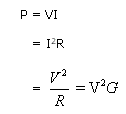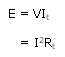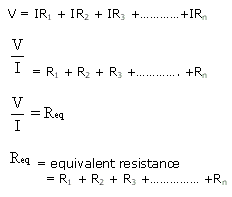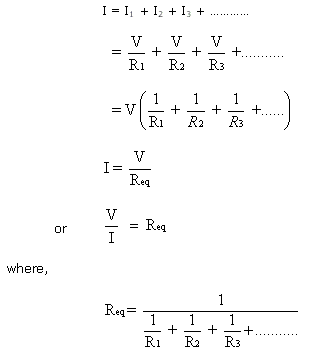Electrical Circuits

Laws of Resistance

1. The resistance of a conductor varies directly as its length.

2. The resistance of a conductor varies inversely to its cross section area.

3. The resistance of a conductor depends on the material.

4. The resistance of a conductor depends on its temperature.

The above factors can be summed up mathematically as :

where ρ is constant representing the nature of material and is known as specific resistance.

Effect of Temperature on Resistance

(a) Resistance of pure metals and alloys increases with rise in temperature.

(b) Resistance of electrolytes, insulators and semiconductors decreases with rise in temperature.

If R_o = Conductor resistance at 0˚C

R_t = Conductor resistance at t˚C

t = rise in temperature

and α_o = Temperature coefficient of resistance at 0˚C,

Then R_t = R_o (1 + α_ot)

The temperature coefficient at 0˚C is defined at the change in resistance per ohm for a rise in temperature of 1˚C from 0˚C.

Grouping of Cells

A single cell has an e.m.f. of about 1.5 volts. If either more voltage is needed or more current is required, then cells are connected either in series or in parallel respectively. This arrangement of connection is named as grouping of cells.

Cells in Series

When cell are connected in series, e.m.f. of the battery is equal to the sum of the e.m.f. of cells.

Internal resistance of battery =sum of internal resistance of cells.

e.m.f. of battery E =ne

where e is e.m.f. of the cell and n refers to the number of cells in series.

Cells in Parallel

The cells when arranged in parallel have the same e.m.f., but internal resistance of the unit is reduced.

If n cells are connected in parallel, each of e.m.f. E,

then

e.m.f. of the battery = e.m.f. of one cell = E

where r is the resistance of one cell

Cells in Series and in Parallel

n = number of cells in each row

m = number of parallel rows.

N = total number of cells = mn.

Let e.m.f of one cell =e

E.M.F. of battery =ne volts

Internal resistance of each row =nr ohms

Cell Efficiency

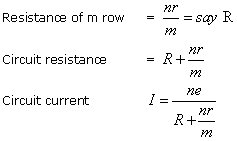
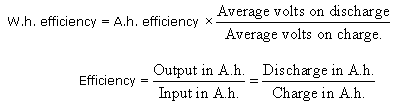
The efficiency of a Cell is considered in two ways:

(1) Ampere-hour (A.h) efficiency.

(2) Watt-hour (W.h.) efficiency.

D.C. Motors

D.C. motors are classified according to the method of excitation. They may be of the shunt, series or compound types.

Series Motor

The speed of a series motor is given by the relation:

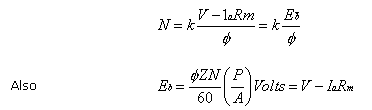
Shunt motor

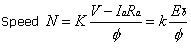
where R_a is the armature resistance. Since is practically constant at all loads, speed is there almost constant.

Types of Armature Winding

The two main types of winding are:

1. Lap Winding. It is also known as parallel winding or multiple winding. In this type of winding, the numbers of parallel paths (A) are equal to the number of poles (P).

2. Wave Winding. In this case the armature conductors are divided into two parallel irrespective of the number of poles.

Slip

The rotor of induction motor rotates at somewhat lesser speed than the synchronous speed and actual speed is known as slip.

where Nr is rotor or actual while N is synchronous speed.

AC through Resistance and Inductance

In the resistance part of the circuit the current is in phase with the voltage, while in the inductive part it is 90˚ out of phase. Hence, to determine the current, the effect of resistance and reactance has to be combined which is named as impedance:

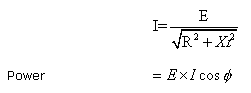
where is the phase angle between the voltage and current and cos is called the power factor.

Circuits Containing Resistance, Inductance and Capacitance

Transformer

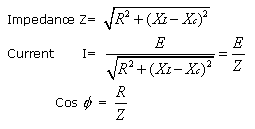
Transformer is a device for transferring energy from one alternating current circuit to another without any change in frequency. It changes voltage from high to low and low to high with a corresponding increase or decrease in current. If the voltage is increased, the transfer is said to be stepped up. If it is decreased, then it is referred as step down.

Three Phase Transformer

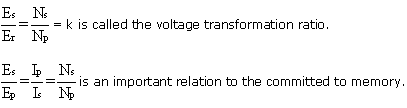
Whenever the supply is three phase and it is desired to transform current at another voltage, then either a single three phase transformer or three separate single phase transformers can be used. However, in practice a single three phase transformer is used. The three phase winding of a transformer can be connected either in star or in delta.

Current and voltage in star

The e.m.f. between any line and the neutral gives the phase voltage while the e.m.f. between two outer terminals is known as line voltage.

Current in each line is the same as phase current

i.e. Line current I_L=Phase current I_P

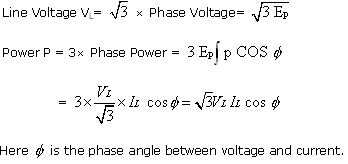
Line Voltage and Current in Delta

Read More

ELECTRICITY

Ohm's Law

where,

I = current, amp

V = potential difference, volts

R = resistance, ohms

Resistivity

where,

ρ = resistivity or specific resistance, ohm-m

L = length of wire, m

A = cross-sectional area of wire, m²

Conductance (G)

where,

γ = conductivity or specific conductance, mhos/m

Electric Power

where,

P = electric power, watts

Electric Energy

where, E = electric energy, Joules

V = potential difference, Volts

I = Current, Amperes

R = resistance, ohms

t = time, seconds

E = 0.24I²Rt, cal

For Battery

where

Kirchhoff’s Law

(i) The algebraic sum of all the currents directed towards a junction point is zero.

(ii) The algebraic sum of all the voltage rise taken in a specified direction around a closed circuit is zero.

Series Circuits:

Parallel Circuits:

Coulomb’s Law

The force acting between two charged bodies q₁ and q₂ in air is proportional to the product of charges and inversely proportional to the square of the distance between them.

Read More

Time Constants Calculation

Capacitance and resistance
The time constant of a capacitance C and a resistance R is equal to CR, and represents the time to change the voltage on the capacitance from zero to E at a constant charging current E / R (which produces a rate of change of voltage E / CR across the capacitance).

Similarly, the time constant CR represents the time to change the charge on the capacitance from zero to CE at a constant charging current E / R (which produces a rate of change of voltage E / CR across the capacitance).

If a voltage E is applied to a series circuit comprising a discharged capacitance C and a resistance R, then after time t the current i, the voltage v_R across the resistance, the voltage v_C across the capacitance and the charge q_C on the capacitance are:
i = (E / R)e ^{- t / CR}
v_R = iR = Ee ^{- t / CR}
v_C = E - v_R = E(1 - e ^{- t / CR})
q_C = Cv_C = CE(1 - e ^{- t / CR})

If a capacitance C charged to voltage V is discharged through a resistance R, then after time t the current i, the voltage v_R across the resistance, the voltage v_C across the capacitance and the charge q_C on the capacitance are:
i = (V / R)e ^{- t / CR}
v_R = iR = Ve ^{- t / CR}
v_C = v_R = Ve ^{- t / CR}
q_C = Cv_C = CVe ^{- t / CR}

Inductance and resistance
The time constant of an inductance L and a resistance R is equal to L / R, and represents the time to change the current in the inductance from zero to E / R at a constant rate of change of current E / L (which produces an induced voltage E across the inductance).

If a voltage E is applied to a series circuit comprising an inductance L and a resistance R, then after time t the current i, the voltage v_R across the resistance, the voltage v_L across the inductance and the magnetic linkage y_L in the inductance are:
i = (E / R)(1 - e ^{- tR / L})
v_R = iR = E(1 - e ^{- tR / L})
v_L = E - v_R = Ee ^{- tR / L}
y_L = Li = (LE / R)(1 - e ^{- tR / L})

If an inductance L carrying a current I is discharged through a resistance R, then after time t the current i, the voltage v_R across the resistance, the voltage v_L across the inductance and the magnetic linkage y_L in the inductance are:
i = Ie ^{- tR / L}
v_R = iR = IRe ^{- tR / L}
v_L = v_R = IRe ^{- tR / L}
y_L = Li = LIe ^{- tR / L}

Rise Time and Fall Time
The rise time (or fall time) of a change is defined as the transition time between the 10% and 90% levels of the total change, so for an exponential rise (or fall) of time constant T, the rise time (or fall time) t_10-90 is:
t_10-90 = (ln0.9 - ln0.1)T » 2.2T

The half time of a change is defined as the transition time between the initial and 50% levels of the total change, so for an exponential change of time constant T, the half time t₅₀ is :
t₅₀ = (ln1.0 - ln0.5)T » 0.69T

Note that for an exponential change of time constant T:
- over time interval T, a rise changes by a factor 1 - e ^-1 (» 0.63) of the remaining change,
- over time interval T, a fall changes by a factor e ^-1 (» 0.37) of the remaining change,
- after time interval 3T, less than 5% of the total change remains,
- after time interval 5T, less than 1% of the total change remains.

Read More

NOTATION Calculations

C E e G I i k L M N P

capacitance voltage source instantaneous E conductance current instantaneous I coefficient inductance mutual inductance number of turns power

[farads, F] [volts, V] [volts, V] [siemens, S] [amps, A] [amps, A] [number] [henrys, H] [henrys, H] [number] [watts, W]

Q q R T t V v W F Y y

charge instantaneous Q resistance time constant instantaneous time voltage drop instantaneous V energy magnetic flux magnetic linkage instantaneous Y

[coulombs, C] [coulombs, C] [ohms, W] [seconds, s] [seconds, s] [volts, V] [volts, V] [joules, J] [webers, Wb] [webers, Wb] [webers, Wb]

Read More