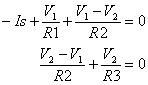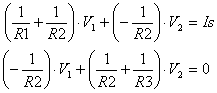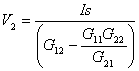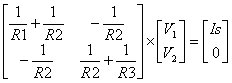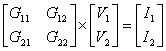Conversion from Decimal to Others

Decimal TO Binary

Comparison with descending powers of two and subtraction

1. List the powers of two in a "base 2 table" from right to left. Start at 2⁰, evaluating it as "1". Increment the exponent by one for each power. The list, to ten elements, would look like this: 512, 256, 128, 64, 32, 16, 8, 4, 2, 1
2. For this example, let's convert the decimal number 156₁₀ to binary. What is the greatest power of two that will fit into 156? Since 128 fits, write a 1 for the leftmost binary digit, and subtract 128 from your decimal number, 156. You now have 28.
3. Move to the next lower power of two. Can 64 fit into 28? No, so write a 0 for the next binary digit to the right.
4. Can 32 fit into 28? No, so write a 0.
5. Can 16 fit into 28? Yes, so write a 1, and subtract 16 from 28. You now have 12.
6. Can 8 fit into 12? Yes, so write a 1, and subtract 8 from 12. You now have 4.
7. Can 4 (power of two) fit into 4 (working decimal)? Yes, so write a 1, and subtract 4 from 4. You have 0.
8. Can 2 fit into 0? No, so write a 0.
9. Can 1 fit into 0? No, so write a 0.
10. Since there are no more powers of two in the list, you are done. You should have 10011100. This is the binary equivalent of the decimal number 156. Or, written with base subscripts: 156₁₀ = 10011100₂

Here is the example of this method written on a piece of paper. The steps are labeled "A" through "L".

Repetition of this method will result in memorization of the powers of two, which will allow you to skip step 1.

Short division by two with remainder

This method is much easier to understand when visualized on paper. It relies only on division by two.

1. For this example, let's convert the decimal number 156₁₀ to binary. Write the decimal number as the dividend inside an upside-down "long division" symbol. Write the base of the destination system (in our case, "2" for binary) as the divisor outside the curve of the division symbol.

   2)156

2. Write the integer answer (quotient) under the long division symbol, and write the remainder (0 or 1) to the right of the dividend.

   2)156 0
   78

3. Continue downwards, dividing each new quotient by two and writing the remainders to the right of each dividend. Stop when the quotient is 1.

   2)156 0
   2)78 0
   2)39 1
   2)19 1
   2)9 1
   2)4 0
   2)2 0
   2)1 1
   2)0 0
   

4. Starting with the bottom 1, read the sequence of 1's and 0's upwards to the top. You should have 10011100. This is the binary equivalent of the decimal number 156. Or, written with base subscripts: 156₁₀ = 10011100₂

Simple Table

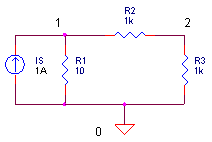
Example:

*

So, we have

displaymath}" border="0" height="31" width="386">

Conversion for FRACTIONAL PART

Read More

Nodal Analysis

Introduction

Kirchoff discovered this: the total current entering a node equals the total current leaving a node! And, these currents can be described by an equation of voltages and conductances. If you have more than one node, then you get more than one equation describing the same system (simultaneous equations). The trick now is finding the voltage at each node that satisfies all of the equations simultaneously.

Circuit Example Here’s a simple circuit example.

Another way of stating the KC Law is this: the sum of currents in and out of a node is zero. This makes writing nodal equations a piece of cake. The two equations for the two circuit nodes look like this.

Because our mission is to calculate the node voltages, let’s reorganize the equations in terms of V1 and V2.

So here sit V1 and V2 in the middle of two different equations. The trick is finding the values of V1 and V2 that satisfy both equations. But how?

SOLUTION #1 – WORK THE EQUATIONS

Just roll up your sleeves and solve for V1 and V2. Before we begin we’ll make bookkeeping easy by writing the resistors in terms of total conductance: G11 = 1/R1 + 1/R2, G12 = -1/R2, G21 = -1/R2 and G22 = 1/R2+1/R3. The system equations now look like this.

First, solve the second equation for V1

Then, stick this into the first equation and solve for V2

Okay, it’s a little messy, but we’ve got V2 described by circuit conductances and Is only! After V2 is calculated numerically, stick it back into V1 = – G22 ∙V2 / G21 and there you have it, circuit voltages V1 and V2 that satisfy both system equations.

SOLUTION #2 – THE MATRIX

Solution #1 looks reasonable for simple circuits, but what about medium or large circuits? The bookkeeping of terms spins out of control quickly. What’s needed is a more methodical and efficient solution: Enter the Matrix. Here’s the set of nodal equations written in matrix form.

Or, in terms of total conductances and source currents

Treating each matrix as a variable, you can write

G ∙ v = i

In the matrix world, you can solve for a variable (almost) like any other algebraic equation. Solving for v you get

v = G^-1∙ i

Where G^-1 is the matrix inverse of G. ( 1 / G does not exist in the matrix world.) This equation is the central mechanism of the SPICE algorithm. Regardless of the analysis – AC, DC, or Transient – all components or their effects are cast into the conductance matrix G and the node voltages are calculated by v = G^-1∙ i , or some equivalent method.

LINEAR DC ANALYSIS

Armed with Nodal Analysis and an Excel spreadsheet, you can perform Linear DC Analysis on the circuit above. Download and open the spreadsheet . Enter the circuit values under the variables shaded light blue.

R1	R2	R3	Is
10	1000	1000	1

How much voltage would you estimate at nodes 1 and 2? You can expect V1 = Is ∙ R1 =
1 A ∙ 10 ohms = 10V. That’s because R2 and R3 have little effect on 10 ohms. At node 2, the simple R2-R3 divider should produce about V2 = 5V.

First, the spread sheet calculates the conductance matrix G

0.101	-0.001
-0.001	0.002

according to the equations

1/R1 + 1/R2	-1/R2
-1/R2	1/R2 + 1/R3

Next, Excel inverts G and multiplies the result G-1 by i to get v. ( See how Excels inverts and multiplies matrices below.)

G^-1 x i = v

9.95	4.98	x	1	=	9.9502
4.98	502.49		0		4.9751

And there you have it, just like the SPICE engine, we’ve computed the circuit’s voltages! Pick other values for R1 like 1 or 100 Ω. Does the output scale up and down as expected? Change R2 or R3. Vary Is or change its polarity.

HANDS-ON DESIGN Try adding another resistor to the circuit. For example, place R4 in parallel with R3. Write out the nodal equations. Then include R3 in the cell formulas that form G. The Excel formulas should effectively calculate the following.

1/R1 + 1/R2	-1/R2
-1/R2	1/R2 + 1/R3 + 1/R4

Read More

Number Systems

Number Systems

Many number systems are in use in digital technology. The most common are the decimal, binary, octal, and hexadecimal systems. The decimal system is clearly the most familiar to us because it is a tool that we use every day. Examining some of its characteristics will help us to better understand the other systems. In the next few pages we shall introduce four numerical representation systems that are used in the digital system. There are other systems, which we will look at briefly.

• Decimal
• Binary
• Octal
• Hexadecimal

Decimal System

The decimal system is composed of 10 numerals or symbols. These 10 symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Using these symbols as digits of a number, we can express any quantity. The decimal system is also called the base-10 system because it has 10 digits.Even though the decimal system has only 10 symbols, any number of any magnitude can be expressed by using our system of positional weighting.

Eg : 23.445, 2335,767.234.

Binary System

In the binary system, there are only two symbols or possible digit values, 0 and 1. This base-2 system can be used to represent any quantity that can be represented in decimal or other base system.The binary number system is the most important one in digital systems, but several others are also important. The decimal system is important because it is universally used to represent quantities outside a digital system. This means that there will be situations where decimal values have to be converted to binary values before they are entered into the digital system

Eg : 1001,101010,11111

Octal System

The octal number system has a base of eight, meaning that it has eight possible digits: 0,1,2,3,4,5,6,7.Although this was once a popular number base, especially in the Digital Equipment Corporation PDP/8 and other old computer systems, it is rarely used today. The Octal system is based on the binary system with a 3-bit boundary.

Eg : 123,765,345.

Hexadecimal System

The hexadecimal system uses base 16. Thus, it has 16 possible digit symbols. It uses the digits 0 through 9 plus the letters A, B, C, D, E, and F as the 16 digit symbols.Hex is just a more human readable version of binary. I would say 11111111 in binary but it is much easier to say FF in hex, which is 255 in decimal by the way. Hex is just a very easy way to remember a group of bits, in this case 4 bits. You might say hex is simply shorthand for binary.

Eg : AC67,F63,689.

Read More

Mesh Analysis

Meshes

A 'mesh' (also called a loop) is simply a path through a circuit that starts and ends at the same place. For the purpose of mesh analysis, a mesh is a loop that does not enclose other loops.

Mesh Analysis

Similar to nodal analysis, mesh analysis is a formalized procedure based on KVL equations. A caveat: mesh analysis can only be used on 'planar' circuits (i.e. there are no crossed, but unconnected, wires in the circuit diagram.)

Steps:

1. Draw circuit in planar form (if possible.)

2. Identify meshes and name mesh currents. Mesh currents should be in the clockwise direction. The current in a branch shared by two meshes is the difference of the two mesh currents.

3. Write a KVL equation in terms of mesh currents for each mesh.

4. Solve the resulting system of equations.

Complication in Mesh Analysis

1. Dependent Voltage Sources

Solution: Same procedure, but write the dependency variable in terms of mesh currents.

2. Independent Current Sources

Solution: If current source is not on a shared branch, then we have been given one of the mesh currents! If it is on a shared branch, then use a 'super-mesh' that encircles the problem branch. To make up for the mesh equation you lose by doing this, use the mesh current relationship implied by the current source (i.e. I₂ − I₁ = 4mA).

3. Dependent Current Sources

Solution: Same procedure as for an independent current source, but with an extra step to eliminate the dependency variable. Write the dependency variable in terms of mesh currents.

Example

Given the Circuit below, find the currents I₁, I₂.

The circuit has 2 loops indicated on the diagram. Using KVL we get:
Loop1: 0 = 9 - 1000I₁ - 3000(I₁ - I₂)
Loop2: 0 = 3000(I₁ - I₂) - 2000I₂ - 2000I₂
Simplifying we get the simultaneous equations:
0 = 9 - 4000I₁ + 3000I₂
0 = 0 + 3000I₁ - 7000I₂
solving to get:
I₁ = 3.32mA
I₂ = 1.42mA

Read More

SIMPLE ELECTRONIC DECISION MAKER

ELECTRONIC DECISION MAKER
A Simple circuit that makes decision for you within a FLASH....
press "S1" to switch on the circuit and then S2 to make a decision.

Circuit Diagram

Parts List

• 1 - 390R
• 2 - 1K2
• 2 -33K
• 2 -100K
• 1 -1N4002 power diode
• 2 - LED
• 2 -0.1uF Capacitor
  
• 2 - BC548 PNP
• 1 - slide switch
• 1 - push button

Read More

TRAFFIC LIGHTS

TRAFFIC LIGHTS

• As well as the 4017 chip you will need a Hex (6) INVERTER and a Quad (4) AND gate chip.
• Don't forget that all three chips need power connected to the correct pins.
• The six diodes are Light Emitting Diodes (LED's).
• The 470k and 4.7 uF control the speed at which the lights change

Read More

Starting Electronics Construction Techniques

Starting Electronics Construction Techniques
As a step-by-step guide from circuit design to finished product, this practical electronics book actually explains how to select the right tools and components for the job, use a soldering iron, etch a printed circuit board and mount the finished product in a case - and puts skills into practice through simple self-build projects.
Whilst most electronics texts focus on theoretical knowledge, Keith Brindley presents a genuinely 'practical' bench guide and reference for electronics experimenters. The straightforward, interactive style of this book makes it ideal for home electronics work and particularly suitable as an introduction to university lab courses for students who are not familiar with hands-on electronics construction. The book also lends itself as a self-contained resource for secondary school and vocational course classroom projects.
* Master the practical techniques of electronics construction, from using a soldering iron to etching a printed circuit board, and mounting the finished product in a case
* Apply practical electronics skills through a series of simple self-build projects
* A bench reference guide to selecting and using the right tools, techniques and components, whatever your project




Click the download button to start
Password : electronicseveryday

Read More

Transistor tester circuit

Transistor tester circuit

Description

Here is a very simple circuit that can b e used to check the hfe of transistors. Both PNP and NPN transistors can be checked using this circuit. Hfe as high as 1000 can be measured by using this circuit.The circuit is based on two constant current sources build around transistors Q1 and Q2.The Q1 is a PNP transistor and the constant current flows in the emitter lead. The value of constant current can be given by the equation; (V D1 -0.6)/ (R2+R4).The POT R4 can be adjusted to get a constant current of 10uA.

The Q2 is an NPN transistor and the constant current flows into the collector lead. The value of this constant current can be given by the equation; (VD2-0.6)/(R3+R5).The POT R5 can be adjusted to get a constant current of 10uA.This constant current provided by the Q1 circuit if the transistor under test is an NPN transistor and by Q2 circuit if the transistor under test is a PNP transistor is fed to the base of transistor under test. This current multiplied by the hfe flows in the collector of the transistor and it will be indicated by the meter. The meter can be directly calibrated to read the hfe of the transistor.

Circuit Diagram

Read More