Multiplexer

Introduction

Multiplexers are used in building digital semiconductor such as CPUs and graphics controllers. In these applications, the number of inputs is generally a multiple of 2 (2, 4, 8, 16, etc.), the number of outputs is either 1 or relatively small multiple of 2, and the number of control signals is related to the combined number of inputs and outputs. For example, a 2-input, 1-output mux requires only 1 control signal to select the input, while a 16-input, 4-output mux requires 4 control signals to select the input and 2 to select the output.

Multiplexers are also used in communications; the telephone network is an example of a very large virtual mux built from many smaller discrete ones. Instead of having a direct connection from every telephone to every telephone - which would be physically impossible - the network "muxes" individual telephones onto one of a small number of wires as calls are placed. At the receiving end, a demultiplexer, or "demux", chooses the correct destination from the many possible destinations by applying the same principle in reverse.

There are more complex forms of multiplexers. Time-division multiplexers, for example, have the same input/output characteristics as described above, but instead of having a control signal, they alternate between all possible inputs at precise time intervals. By taking turns in this manner, many inputs can share one output. This technique is commonly used on long distance phone lines, allowing many individual phone calls to be spliced together without affecting the speed or quality of any individual call. Time-division multiplexers are generally built as semiconductor devices, or chips, but can also be built as optical devices for fiber optics applications.

Even more complex are code-division multiplexers. Using mathematical techniques developed during World War II for cryptographic purposes, they have since found application in modern cellular networks. Generally referred to by the acronim "CDMA" - Code Division Multiple Access - these semiconductor devices work by assigning each input a unique complex mathematical code. Each input applies its code to the signal it receives, and all signals are simultaneously sent to the output. At the receiving end, a demux performs the inverse mathematical operation to extract the original signals.

Example

The circuit symbol for the above multiplexer is:

Two input multiplexer

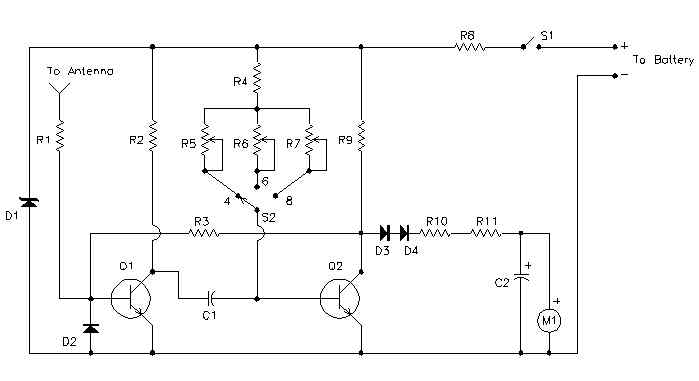
One circuit I've received a number of requests for is the multiplexer circuit. This is a digital circuit with multiple signal inputs, one of which is selected by separate address inputs to be sent to the single output. It's not easy to describe without the logic diagram, but is easy to understand when the diagram is available.

The multiplexer circuit is typically used to combine two or more digital signals onto a single line, by placing them there at different times. Technically, this is known as time-division multiplexing.

Input A is the addressing input, which controls which of the two data inputs, X0 or X1, will be transmitted to the output. If the A input switches back and forth at a frequency more than double the frequency of either digital signal, both signals will be accurately reproduced, and can be separated again by a demultiplexer circuit synchronized to the multiplexer.

This is not as difficult as it may seem at first glance; the telephone network combines multiple audio signals onto a single pair of wires using exactly this technique, and is readily able to separate many telephone conversations so that everyone's voice goes only to the intended recipient. With the growth of the Internet and the World Wide Web, most people have heard about T1 telephone lines. A T1 line can transmit up to 24 individual telephone conversations by multiplexing them in this manner.

A very common application for this type of circuit is found in computers, where dynamic memory uses the same address lines for both row and column addressing. A set of multiplexers is used to first select the row address to the memory, then switch to the column address. This scheme allows large amounts of memory to be incorporated into the computer while limiting the number of copper traces required to connect that memory to the rest of the computer circuitry. In such an application, this circuit is commonly called a data selector.

Multiplexers are not limited to two data inputs. If we use two addressing inputs, we can multiplex up to four data signals. With three addressing inputs, we can multiplex eight signals.

Read More

K-Map Minimising

Software to evaluate K-Map
This is a software to minimize a k-map using graphical interface and it can solve k-maps from 3-8 variables.


Click for better Quality...


Click the download button to start
Password : electronicseveryday

Read More

K-Map

Karnaugh Map (K-Map)
A Karnaugh Map is a method of mapping truth tables onto a matrix that identifies places where two or more different combination of the input variables yield the same result. In addition to identifying redundant terms, the K map also cancels them, leaving only the minimized Boolean algebra expressions that will yield the same truth table outputs as the unreduced terms. The best way to understand K maps is to go through an actual simplification process using a K map.

We will start with a three variable truth table. Three variables have 2 to the 3'd, or 8 possible combination of 1’s and 0's. This means that the K map must have 8 cells, one for even possible combination of input variables. The input variables can be mapped in any order on the K map, but it must follow the same organization as the truth table being mapped. We will assign the letters R, S, & T to the input variables of our truth table, and X to the output.

The Karnaugh map is laid out so that from cell to cell and from edge to edge, there is only a one bit change in the variables at any given time. This accounts for the column to column and row to row order of 00 01 11 10 (Gray Code). The column variables are assigned across the top of
the map, and the row variables are assigned to the left side of the map. Each cell contains the result of the variables for the binary combination given by the intersecting row and column. If the column variables are R S and the row variables are T U for a 16 cell or four variable map, the combination 0 1 1 0 is the same as (not R S T not U) or cell 6. If the truth table shows a 1 for the output at the position 0 1 1 0, then the Karnaugh map will contain a 1 in that particular cell.

As an example, Let's simplify the 3 bit K map above. Notice the four three variable expressions reduce down to three two variable expressions. This is a substantial savings in circuitry, and the equation will do exactly the same thing as the original unsimplified expression from the truth table.

The same method applies to larger K maps of 4, 5, and 6 variables. Four variable K maps have sixteen cells, since 2 to the 4 is 16. Five variable K maps are mapped as two, sixteen cell maps side by side. It is like mapping one map above the other, with the same numbered cells being redundant. Six variable K maps result in four, sixteen cell maps together in a square pattern. Top to bottom and side by side, redundancies are cancelled in the same numbered cells. More than four variable K maps are rarely used because they are more difficult to follow without getting lost.

Read More

Wireless auto tachometer

INTRODUCTION
Anyone performing their own automobile tune-ups knows how important it is to know your engines speed. With this tachometer, you can measure your engines speed without any connections or annoying timing lights.

circuit diagram

Notes

1. Calibrate the unit as folows:
1. Set up this circuit:

   

2. Turn on the Tach and allow a few minutes for temperature stabilization.
3. Set S2 to 4 cylinders and adjust R5 for a meter indication of 180 (1800 rpm).
4. Set S2 to 6 cylinders and adjust R6 for a meter indication of 120 (1200 rpm).
5. Set S2 to 8 cylinders and adjust R7 for a meter indication of 90 (900 rpm).
2. To use the Tach, turn it on and let it sit for one minute to allow for temperature stabilization. Extend the antenna, select the right number of cylinders and hold the unit over the engine. If the reading is erratic or the needle jumps around, move the antenna closer to the ignition coil or spark plug wires.

The unit draws power from the car battery. If it is connected backwards, it will not work, but it won't be damaged.

parts required

Part	Total Qty.	Description	Substitutions
C1	1	0.47uF Capacitor
C2	1	47uF Electrolytic Capacitor
D1	1	8V 1W Zener Diode
D2, D3, D4	3	1N914 Diode
M1	1	200uA Meter
Q1, Q2	2	2N3391A Transistor
R1, R2, R9	3	1K 1/2 W Resistor
R3	1	47K 1/2 W Resistor
R4	1	10K 1/2 W Resistor
R5, R6	2	25K Trim Pot
R7	1	10K Trim Pot
R8	1	200 Ohm 2 W Resistor
R10	1	15K 1/2 W Resistor
R11	1	2.2K 1/2 W Resistor
S1	1	SPST Togglae Switch
S2	1	Three Position Single Pole Rotary Switch
MISC	1	Telescoping Radio Antenna, Enclosure, Power Cable and Battery Connector

Read More

Semi Log Graph Sheet

Semi Log Graph

They are mainly used for plotting very LARGE and very SMALL value in a same graph
Notice that the numbers along the x axis are evenly spaced, while along the y-axis, we have powers of 10 evenly spaced.

Taking the section between 1 and 10


Finding Slope on Semi Log Graph

Read More

Conversion of Binary to Decimal

binary to decimal...

introduction:-

The binary (base two) numeral system has two possible values, often represented as 0 or 1, for each place-value. In contrast, the decimal (base ten) numeral system has ten possible values (0,1,2,3,4,5,6,7,8, or 9) for each place-value.

To avoid confusion while using different numeral systems, the base of each individual number may be specified by writing it as a subscript of the number. For example, the binary number 10011100 may be specified as "base two" by writing it as 10011100₂. The decimal number 156 may be written as 156₁₀ and read as "one hundred fifty-six, base ten".

STEPS:-

1. 1. For this example, let's convert the binary number 10011011₂ to decimal. List the powers of two from right to left. Start at 2⁰, evaluating it as "1". Increment the exponent by one for each power. Stop when the amount of elements in the list is equal to the amount of digits in the binary number. The example number, 10011011, has eight digits, so the list, to eight elements, would look like this: 128, 64, 32, 16, 8, 4, 2, 1
   2. Write the binary number below the list.
   3. 
      

      Here is this step written on paper using the example binary number, 10011011.
   4. Draw lines, starting from the right, connecting each consecutive digit of the binary number to the power of two that is next in the list above it. Begin by drawing a line from the first digit of the binary number to the first power of two in the list above it. Then, draw a line from the second digit of the binary number to the second power of two in the list. Continue connecting each digit with its corresponding power of two.
      
      
      

      Here is this step written on paper using the example binary number, 10011011.
   5. Move through each digit of the binary number. If the digit is a 1, write its corresponding power of two below the line, under the digit. If the digit is a 0, write a 0 below the line, under the digit.
      
      
      

      Here is this step written on paper using the example binary number, 10011011.
   6. Add the numbers written below the line. The sum should be 155. This is the decimal equivalent of the binary number 10011011. Or, written with base subscripts: 10011011₂ = 155₁₀
      
      
      
      

      Here is this step written on paper using the example binary number, 10011011. The sum of the bottom row, 155, is its decimal equivalent. Or, written with base subscripts: 10011011₂ = 155₁₀
   7. Repetition of this method will result in memorization of the powers of two, which will allow you to skip step 1.
   Doubling method

   Starting from zero, and working from left to right, double your number and add the next digit of the base two representation. For example to convert 1011001, we take the following steps.

   1. 1|011001 0*2+1 = 1
   2. 10|11001 1*2+0 = 2
   3. 101|1001 2*2+1 = 5
   4. 1011|001 5*2+1 = 11
   5. 10110|01 11*2+0 = 22
   6. 101100|1 22*2+0 = 44

7.1011001 44*2+1 = 89

Tips

• Practice. Try converting the binary numbers 11010001₂, 11001₂, and 11110001₂. Respectively, their decimal equivalents are 209₁₀, 25₁₀, and 241₁₀.
• The calculator that comes installed with Microsoft Windows can do this conversion for you, but as a programmer, you're better off with a good understanding of how the conversion works. The calculator's conversion options can be made visible by opening its "View" menu and selecting "Scientific". On Linux, you can use galculator.
• There is another way to convert from binary to decimal, which ignores the binary values of the columns. Take the left-most one digit and start there as "1." For each column to the right, double your subtotal and add the next digit. For example, "1011" would entail the following: "1," (double) 2, (add 0) 2, (double) 4, (add 1) 5, (double) 10, and finally (add 1) 11. This technique is very useful for converting large numbers in your head, as you only need to keep track of your sub-total (you are simply adding and doubling).

Read More

Conversion from Decimal to Others

Decimal TO Binary

Comparison with descending powers of two and subtraction

1. List the powers of two in a "base 2 table" from right to left. Start at 2⁰, evaluating it as "1". Increment the exponent by one for each power. The list, to ten elements, would look like this: 512, 256, 128, 64, 32, 16, 8, 4, 2, 1
2. For this example, let's convert the decimal number 156₁₀ to binary. What is the greatest power of two that will fit into 156? Since 128 fits, write a 1 for the leftmost binary digit, and subtract 128 from your decimal number, 156. You now have 28.
3. Move to the next lower power of two. Can 64 fit into 28? No, so write a 0 for the next binary digit to the right.
4. Can 32 fit into 28? No, so write a 0.
5. Can 16 fit into 28? Yes, so write a 1, and subtract 16 from 28. You now have 12.
6. Can 8 fit into 12? Yes, so write a 1, and subtract 8 from 12. You now have 4.
7. Can 4 (power of two) fit into 4 (working decimal)? Yes, so write a 1, and subtract 4 from 4. You have 0.
8. Can 2 fit into 0? No, so write a 0.
9. Can 1 fit into 0? No, so write a 0.
10. Since there are no more powers of two in the list, you are done. You should have 10011100. This is the binary equivalent of the decimal number 156. Or, written with base subscripts: 156₁₀ = 10011100₂

Here is the example of this method written on a piece of paper. The steps are labeled "A" through "L".

Repetition of this method will result in memorization of the powers of two, which will allow you to skip step 1.

Short division by two with remainder

This method is much easier to understand when visualized on paper. It relies only on division by two.

1. For this example, let's convert the decimal number 156₁₀ to binary. Write the decimal number as the dividend inside an upside-down "long division" symbol. Write the base of the destination system (in our case, "2" for binary) as the divisor outside the curve of the division symbol.

   2)156

2. Write the integer answer (quotient) under the long division symbol, and write the remainder (0 or 1) to the right of the dividend.

   2)156 0
   78

3. Continue downwards, dividing each new quotient by two and writing the remainders to the right of each dividend. Stop when the quotient is 1.

   2)156 0
   2)78 0
   2)39 1
   2)19 1
   2)9 1
   2)4 0
   2)2 0
   2)1 1
   2)0 0
   

4. Starting with the bottom 1, read the sequence of 1's and 0's upwards to the top. You should have 10011100. This is the binary equivalent of the decimal number 156. Or, written with base subscripts: 156₁₀ = 10011100₂

Simple Table

Example:

*

So, we have

displaymath}" border="0" height="31" width="386">

Conversion for FRACTIONAL PART

Read More